2002 AMC amc8 真题 答案 详解
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2002-amc8-paper-eng-zh.pdf | 11 页 | 446.56KB | 中英双语真题 |
| 2 | 2002-amc8-paper-eng.pdf | 4 页 | 154.48KB | 英文真题 |
| 3 | 2002-amc8-key.pdf | 1 页 | 56.13KB | 真题答案 |
| 4 | 2002-amc8-solution-eng.pdf | 13 页 | 526.92KB | 真题文字详解(英文) |
| 5 | 2002-amc8-solution-eng-zh.pdf | 18 页 | 646.87KB | 真题文字详解(中英双语) |
| 6 | 2002-amc8-solution-video-zh.mp4 | 18.4 分钟 | 47.79MB | 真题视频详解(普通话) |
中英双语真题
2002 AMC8
Problem 1
A circle and two distinct lines are drawn on a sheet of paper. What is the largest possible number of points of intersection of these figures?
在一张纸上画了一个圆和2条不同的直线,则这些图形的交点最多有多少个?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
Problem 2
How many different combinations of $5 bills and $2 bills can be used to make a total of $17? Order does not matter in this problem.
有多少种方法可以将若干张5元纸币和2元纸币组成总额为17元?这道题里不考虑顺序。
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
Problem 3
What is the smallest possible average of four distinct positive even integers?
4 个不同的正偶数的平均值最小可能是多少?
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
Problem 4
The year 2002 is a palindrome (a number that reads the same from left to right as it does from right to left). What is the product of the digits of the next year after 2002 that is a palindrome?
2002 年这个年份的数字是个回环数(是一个从左向右读和从右向左读一样的数)。那么 2002 年之后的下一个也是回环数的年份的各个位上数字之积是多少?
(A) 0 (B) 4 (C) 9 (D) 16 (E) 25

英文真题
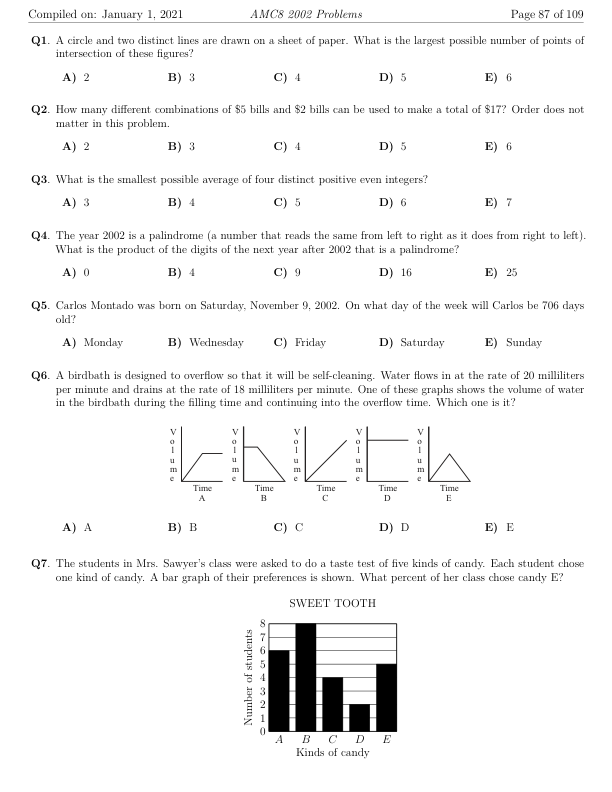
Compiled on: January 1, 2021 AMC8 2002 Problems Page 87 of 109 Q1. A circle and two distinct lines are drawn on a sheet of paper. What is the largest possible number of points of intersection of these figures? A) 2 B) 3 C) 4 D) 5 E) 6 Q2. How many different combinations of $5 bills and $2 bills can be used to make a total of $17? Order does not matter in this problem. A) 2 B) 3 C) 4 D) 5 E) 6 Q3. What is the smallest possible average of four distinct positive even integers? A) 3 B) 4 C) 5 D) 6 E) 7 Q4. The year 2002 is a palindrome (a number that reads the same from left to right as it does from right to left). What is the product of the digits of the next year after 2002 that is a palindrome? A) 0 B) 4 C) 9 D) 16 E) 25 Q5. Carlos Montado was born on Saturday, November 9, 2002. On what day of the week will Carlos be 706 days old? A) Monday B) Wednesday C) Friday D) Saturday E) Sunday Q6. A birdbath is designed to overflow so that it will be self-cleaning. Water flows in at the rate of 20 milliliters per minute and drains at the rate of 18 milliliters per minute. One of these graphs shows the volume of water in the birdbath during the filling time and continuing into the overflow time. Which one is it? A) A B) B C) C D) D E) E Q7. The students in Mrs. Sawyer's class were asked to do a taste test of five kinds of candy. Each student chose one kind of candy. A bar graph of their preferences is shown. What percent of her class chose candy E? SWEET TOOTH Number of students 8 7 6 5 4 3 2 1 0 A B C D E Kinds of candy
真题文字详解(英文)
Problem 1
A circle and two distinct lines are drawn on a sheet of paper. What is the largest possible number of points of intersection of these figures?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
Solution
The two lines can both intersect the circle twice, and can intersect each other once, so $2 + 2 + 1 = \boxed{(D) 5}$.
Problem 2
How many different combinations of $5 bills and $2 bills can be used to make a total of $17? Order does not matter in this problem.
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
Solution
https://youtu.be/Zhsb5lv6jCI?t=701
Problem 3
What is the smallest possible average of four distinct positive even integers?
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
Solution
In order to get the smallest possible average, we want the 4 even numbers to be as small as possible. The first 4 positive even numbers are 2, 4, 6, and 8. Their average is $\frac{2+4+6+8}{4}=\frac{20}{4}=\boxed{(C) 5}$.
Problem 4
The year 2002 is a palindrome (a number that reads the same from left to right as it does from right to left). What is the product of the digits of the next year after 2002 that is a palindrome?
(A) 0 (B) 4 (C) 9 (D) 16 (E) 25
Solution 1
The palindrome right after 2002 is 2112. The product of the digits of 2112 is $\boxed{(B) 4}$.
Solution 2
The palindrome formula is to add 110 to the number in order to get the next palindrome, a palindrome needs to be in the form as ABBA. We can use this in this case to get 2112. $211*2=4$. Therefore, the answer is $\boxed{(B) 4}$.
Problem 5
Carlos Montado was born on Saturday, November 9, 2002. On what day of the week will Carlos be 706 days old?
(A) Monday (B) Wednesday (C) Friday (D) Saturday (E) Sunday

真题文字详解(中英双语)
Problem 1
A circle and two distinct lines are drawn on a sheet of paper. What is the largest possible number of points of intersection of these figures?
在一张纸上画了一个圆和两条不同的直线。这些图形最多可能有多少个交点?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
Solution
The two lines can both intersect the circle twice, and can intersect each other once, so 2 + 2 + 1 = \boxed{(D) 5}.
这两条直线都可以与圆相交两次,并且可以相互相交一次,所以 2 + 2 + 1 = \boxed{(D) 5}.
Problem 2
How many different combinations of $5 bills and $2 bills can be used to make a total of $17? Order does not matter in this problem.
可以用多少种不同的$5钞票和$2元钞票的组合来凑出17元?这个问题中,顺序不重要。
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
Solution
https://youtu.be/Zhsb5lv6jCl?t=701
Problem 3
What is the smallest possible average of four distinct positive even integers?
四个不同的正偶数的和的最小可能平均值是多少?
(A) 3 (B) 4 (C) 5 (D) 6 (E) 7
Solution
In order to get the smallest possible average, we want the 4 even numbers to be as small as possible. The first 4 positive even numbers are 2, 4, 6, and 8. Their average is \frac{2+4+6+8}{4} = \frac{20}{4} = \boxed{(C) 5}.
为了得到最小的平均数,我们希望这4个偶数尽可能小。前4个正偶数是2、4、6和8。它们的平均值是\frac{2+4+6+8}{4} = \frac{20}{4} = \boxed{(C) 5}。
Problem 4
The year 2002 is a palindrome (a number that reads the same from left to right as it does from right to left). What is the product of the digits of the next year after 2002 that is a palindrome?
2002年是一个回文数(一个从左到右读和从右到左读都一样的数)。问:2002年之后的下一个回文数的各位数字之积是多少?
(A) 0 (B) 4 (C) 9 (D) 16 (E) 25

