2021 AMC FALL amc10b 真题 答案 详解
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2021-FALL-amc10b-paper-eng-zh.pdf | 12 页 | 539.33KB | 中英双语真题 |
| 2 | 2021-FALL-amc10b-paper-eng.pdf | 5 页 | 244.42KB | 英文真题 |
| 3 | 2021-FALL-amc10b-key.pdf | 1 页 | 10.47KB | 真题答案 |
| 4 | 2021-FALL-amc10b-solution-eng.pdf | 42 页 | 3.49MB | 真题文字详解(英文) |
| 5 | 2021-FALL-amc10b-solution-eng-zh.pdf | 62 页 | 3.82MB | 真题文字详解(中英双语) |
中英双语真题
2021Fall AMC 10B
Problem 1
What is the value of (1234 + 2341 + 3412 + 4123) ?
表达式 (1234 + 2341 + 3412 + 4123 ) 的值是多少?
(A) 10,000 (B) 10,010 (C) 10,110 (D) 11,000 (E) 11,110
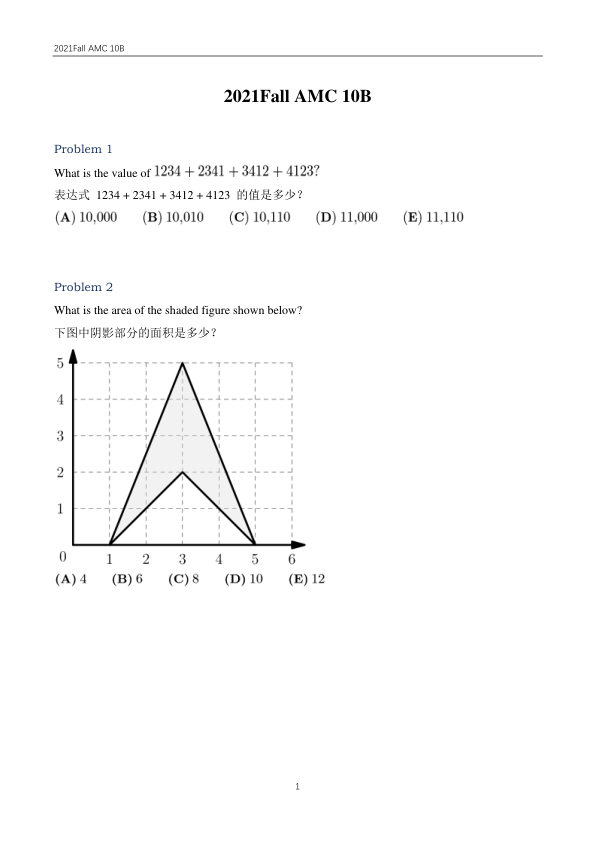
Problem 2
What is the area of the shaded figure shown below?
下图中阴影部分的面积是多少?
(A) 4 (B) 6 (C) 8 (D) 10 (E) 12
英文真题
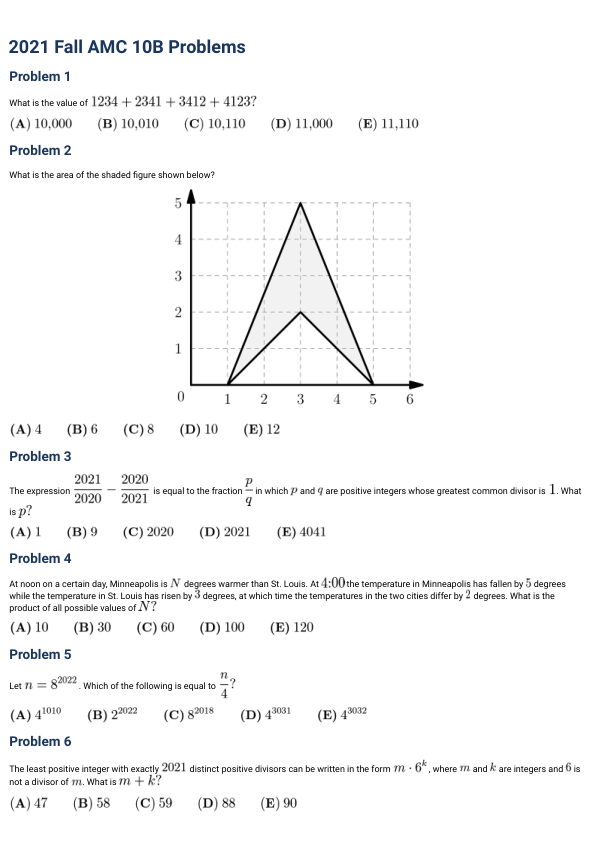
2021 Fall AMC 10B Problems Problem 1 What is the value of $1234 + 2341 + 3412 + 4123$?
(A) 10,000 (B) 10,010 (C) 10,110 (D) 11,000 (E) 11,110
Problem 2 What is the area of the shaded figure shown below?
(A) 4 (B) 6 (C) 8 (D) 10 (E) 12
Problem 3 The expression $\frac{2021}{2020} - \frac{2020}{2021}$ is equal to the fraction $\frac{p}{q}$ in which $p$ and $q$ are positive integers whose greatest common divisor is 1. What is $p$?
(A) 1 (B) 9 (C) 2020 (D) 2021 (E) 4041
Problem 4 At noon on a certain day, Minneapolis is $N$ degrees warmer than St. Louis. At 4:00 the temperature in Minneapolis has fallen by 5 degrees while the temperature in St. Louis has risen by 3 degrees, at which time the temperatures in the two cities differ by 2 degrees. What is the product of all possible values of $N$?
(A) 10 (B) 30 (C) 60 (D) 100 (E) 120
Problem 5 Let $n = 8^{2022}$. Which of the following is equal to $\frac{n}{4}$?
(A) $4^{1010}$ (B) $2^{2022}$ (C) $8^{2018}$ (D) $4^{3031}$ (E) $4^{3032}$
Problem 6 The least positive integer with exactly 2021 distinct positive divisors can be written in the form $m\cdot 6^k$, where $m$ and $k$ are integers and 6 is not a divisor of $m$. What is $m+k$?
(A) 47 (B) 58 (C) 59 (D) 88 (E) 90
真题文字详解(英文)
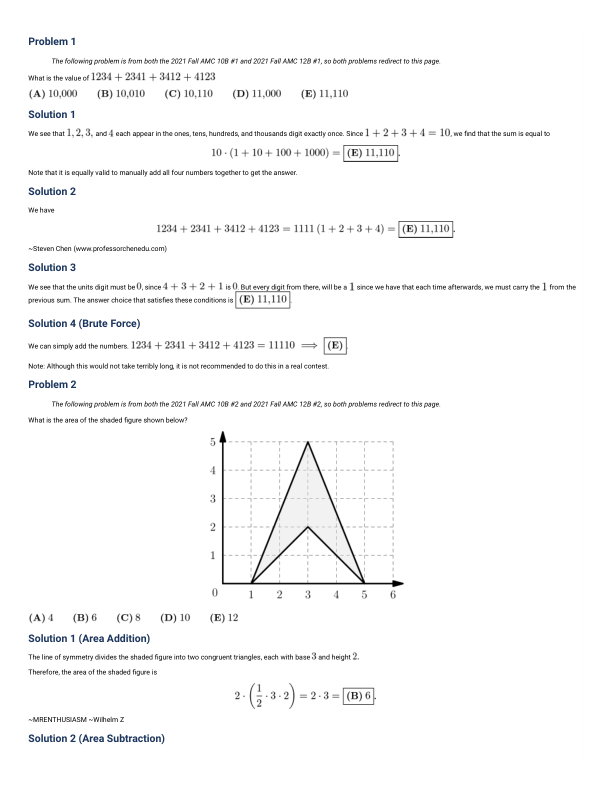
Problem 1 The following problem is from both the 2021 Fall AMC 10B #1 and 2021 Fall AMC 12B #1, so both problems redirect to this page. What is the value of $1234+2341+3412+4123$
(A) 10,000 (B) 10,010 (C) 10,110 (D) 11,000 (E) 11,110 Solution 1 We see that 1, 2, 3, and 4 each appear in the ones, tens, hundreds, and thousands digit exactly once. Since $1 + 2 + 3 + 4 = 10$, we find that the sum is equal to $10 \cdot (1 + 10 + 100 + 1000) =$ (E) 11,110 Note that it is equally valid to manually add all four numbers together to get the answer. Solution 2 We have $1234 + 2341 + 3412 + 4123 = 1111(1 + 2 + 3 + 4) =$ (E) 11,110 ~Steven Chen (www.professorchenedu.com) Solution 3 We see that the units digit must be 0, since $4 + 3 + 2 + 1$ is 0. But every digit from there will be a 1 since we have that each time afterwards, we must carry the 1 from the previous sum. The answer choice that satisfies these conditions is (E) 11,110 Solution 4 (Brute Force) We can simply add the numbers. $1234 + 2341 + 3412 + 4123 = 11110 \Rightarrow$ (E) Note: Although this would not take terribly long, it is not recommended to do this in a real contest. Problem 2 The following problem is from both the 2021 Fall AMC 10B #2 and 2021 Fall AMC 12B #2, so both problems redirect to this page. What is the area of the shaded figure shown below? Solution 1 (Area Addition) The line of symmetry divides the shaded figure into two congruent triangles, each with base 3 and height 2. Therefore, the area of the shaded figure is $2 \cdot \left(\frac{1}{2} \cdot 3 \cdot 2\right) = 2 \cdot 3 =$ (B) 6 ~MRENTHUSIASM ~Wilhelm Z Solution 2 (Area Subtraction)
真题文字详解(中英双语)
Problem 1 The following problem is from both the 2021 Fall AMC 10B #1 and 2021 Fall AMC 12B #1, so both problems redirect to this page. What is the value of $1234 + 2341 + 3412 + 4123$?
(A) 10,000 (B) 10,010 (C) 10,110 (D) 11,000 (E) 11,110 Solution 1 We see that 1, 2, 3, and 4 each appear in the ones, tens, hundreds, and thousands digit exactly once. Since $1+2+3+4=10$, we find that the sum is equal to $10\cdot(1+10+100+1000)=\boxed{(E) 11,110}$. Note that it is equally valid to manually add all four numbers together to get the answer. Solution 2 We have $1234 + 2341 + 3412 + 4123 = 1111(1+2+3+4)=\boxed{(E) 11,110}.$ Solution 3 We see that the units digit must be 0, since $4+3+2+1=0$. But every digit from there will be a 1 since we have that each time afterwards, we must carry the 1 from the previous sum. The answer choice that satisfies these conditions is $\boxed{(E) 11,110}$. Solution 4 (Brute Force) 解法 4 (暴力法) We can simply add the numbers. $1234 + 2341 + 3412 + 4123 = 11110 \implies \boxed{(E)}$. Note: Although this would not take terribly long, it is not recommended to do this in a real contest. Problem 2 The following problem is from both the 2021 Fall AMC 10B #2 and 2021 Fall AMC 12B #2, so both problems redirect to this page.

