2021 AMC amc12a 真题 答案 详解
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2021-amc12a-paper-eng-zh.pdf | 12 页 | 450.41KB | 中英双语真题 |
| 2 | 2021-amc12a-paper-eng.pdf | 4 页 | 238.20KB | 英文真题 |
| 3 | 2021-amc12a-key.pdf | 1 页 | 20.30KB | 真题答案 |
| 4 | 2021-amc12a-solution-eng.pdf | 66 页 | 3.12MB | 真题文字详解(英文) |
| 5 | 2021-amc12a-solution-eng-zh.pdf | 77 页 | 4.36MB | 真题文字详解(中英双语) |
| 6 | 2021-amc12a-solution-video-zh.mp4 | 67.45 分钟 | 153.61MB | 真题视频详解(普通话) |
中英双语真题
2021Spring AMC 12A
Problem 1
What is the value of (2^{1+2+3} - (2^1 + 2^2 + 2^3))?
下式的值是多少
(2^{1+2+3} - (2^1 + 2^2 + 2^3))?
(A) 0 (B) 50 (C) 52 (D) 54 (E) 57
Problem 2
Under what conditions does (\sqrt{a^2+b^2}=a+b) hold, where (a) and (b) are real numbers?
已知 (a) 和 (b) 是实数,问在何种情况下,(\sqrt{a^2+b^2}=a+b) 成立?
(A) It is never true. 永远不成立。
(B) It is true if and only if (ab=0.) 当且仅当 (ab=0) 时才成立。
(C) It is true if and only if (a+b\geqslant 0.) 当且仅当 (a+b\geqslant 0) 时才成立。
(D) It is true if and only if (ab=0) and (a+b\geqslant 0.) 当且仅当 (ab=0) 且 (a+b\geqslant 0) 时才成立。
(E) It is always true. 总是成立。
Problem 3
The sum of two natural numbers is 17,402. One of the two numbers is divisible by 10. If the units digit of that number is erased, the other number is obtained. What is the difference of these two numbers?
两个自然数之和是 17,402。这两个数中的一个可以被 10 整除。如果去掉该数的个位数字则得到另外一个数。问这两个数的差是多少?
(A) 10,272 (B) 11,700 (C) 13,362 (D) 14,238 (E) 15,426

英文真题
2021 AMC 12A Problems Problem 1 What is the value of (2^{1+2+3} - \left(2^1 + 2^2 + 2^3\right))?
(A) 0 (B) 50 (C) 52 (D) 54 (E) 57
Problem 2 Under what conditions is (\sqrt{a^2+b^2}=a+b) true, where (a) and (b) are real numbers?
(A) It is never true.
(B) It is true if and only if (ab=0).
(C) It is true if and only if (a+b \geq 0).
(D) It is true if and only if (ab=0) and (a+b \geq 0).
(E) It is always true.
Problem 3 The sum of two natural numbers is 17,402. One of the two numbers is divisible by 10. If the units digit of that number is erased, the other number is obtained. What is the difference of these two numbers?
(A) 10,272 (B) 11,700 (C) 13,362 (D) 14,238 (E) 15,426
Problem 4 Tom has a collection of 13 snakes, 4 of which are purple and 5 of which are happy. He observes that
- all of his happy snakes can add,
- none of his purple snakes can subtract,
- all of his snakes that can't subtract also can't add.
Which of these conclusions can be drawn about Tom's snakes?
(A) Purple snakes can add.
(B) Purple snakes are happy.
(C) Snakes that can add are purple.
(D) Happy snakes are not purple.
(E) Happy snakes can't subtract.
Problem 5 When a student multiplied the number 66 by the repeating decimal,
[1.\overline{ab}]
where (a) and (b) are digits, he did not notice the notation and just multiplied 66 times (1.ab). Later he found that his answer is 0.5 less than the correct answer. What is the 2-digit number (ab)?
(A) 15 (B) 30 (C) 45 (D) 60 (E) 75

真题文字详解(英文)
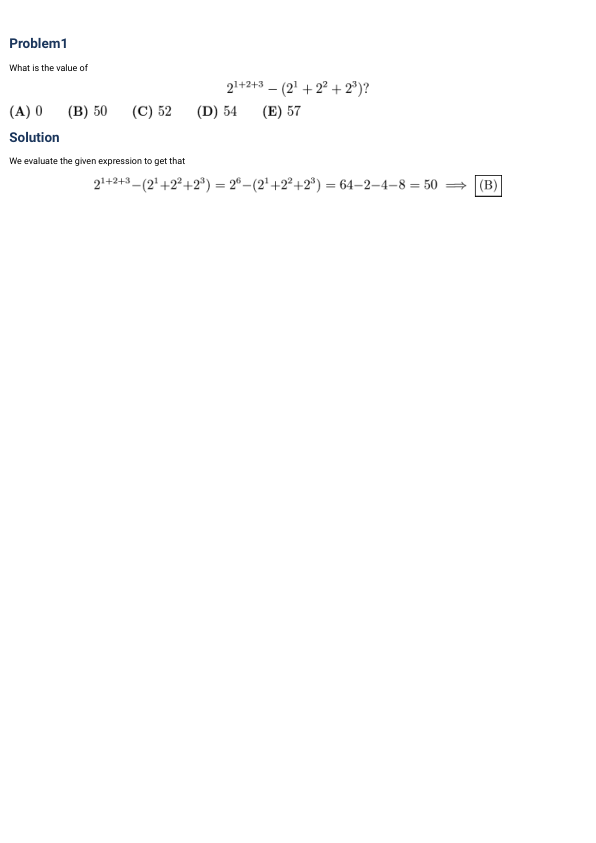
Problem 1 What is the value of $$2^{1+2+3} - (2^1 + 2^2 + 2^3)?$$
(A) 0 (B) 50 (C) 52 (D) 54 (E) 57
Solution We evaluate the given expression to get that $$2^{1+2+3} - (2^1 + 2^2 + 2^3) = 2^6 - (2^1 + 2^2 + 2^3) = 64 - 2 - 4 - 8 = 50 \Rightarrow (B)$$
真题文字详解(中英双语)
Problem 1 What is the value of $$2^{1+2+3} - \left(2^1 + 2^2 + 2^3\right)?$$
(A) 0 (B) 50 (C) 52 (D) 54 (E) 57
Solution We evaluate the given expression to get that $$2^{1+2+3} - \left(2^1 + 2^2 + 2^3\right) = 2^6 - \left(2^1 + 2^2 + 2^3\right) = 64 - 2 - 4 - 8 = 50 \Rightarrow (B)$$
Problem 2 Under what conditions is $$\sqrt{a^2 + b^2} = a + b$$ true, where (a) and (b) are real numbers?
在什么条件下 $$\sqrt{a^2 + b^2} = a + b$$ 为真,其中 (a) 和 (b) 是实数?
(A) It is never true.
(B) It is true if and only if (ab = 0).
(C) It is true if and only if (a + b \geq 0).
(D) It is true if and only if (ab = 0) and (a + b \geq 0).
(E) It is always true.
Solution 1 (Algebra) 解法 1(代数)
One can square both sides to get $$a^2 + b^2 = a^2 + 2ab + b^2$$. Then, $$0 = 2ab \Rightarrow ab = 0$$. Also, it is clear that both sides of the equation must be nonnegative. The answer is (D).
可以对两边同时平方得到 $$a^2 + b^2 = a^2 + 2ab + b^2$$。然后,$$0 = 2ab \Rightarrow ab = 0$$。显然,等式两边的值必须是非负的。答案是 (D)。
Solution 2 (Algebra) 解法 2(代数)
Complete the square of the left side by rewriting the radical to be $$\sqrt{(a+b)^2 - 2ab}$$.
From there it is evident for the square root of the left to be equal to the right, $$ab$$ must be equal to zero. Also, we know that the equivalency of square root values only holds true for nonnegative values of $$a + b$$, making the correct answer (D).
通过将左边的平方根重写为完成左边的平方。从那里可以看出,为了使左边的平方根等于右边,$$ab$$ 必须等于零。我们还知道,平方根的等价性只对 $$a + b$$ 的非负值成立,因此正确的答案是 (D)。
Solution 3 (Process of Elimination) 解法 3(排除法)

