2022 AMC amc12a 真题 答案 详解
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2022-amc12a-paper-eng-zh.pdf | 10 页 | 1.34MB | 中英双语真题 |
| 2 | 2022-amc12a-paper-eng.pdf | 4 页 | 212.88KB | 英文真题 |
| 3 | 2022-amc12a-key.pdf | 1 页 | 9.93KB | 真题答案 |
| 4 | 2022-amc12a-solution-eng.pdf | 49 页 | 3.21MB | 真题文字详解(英文) |
| 5 | 2022-amc12a-solution-eng-zh.pdf | 71 页 | 3.56MB | 真题文字详解(中英双语) |
中英双语真题
2022 AMC 12A
- What is the value of the below expression? 问下式的值是多少?
3 + \frac{1}{3 + \frac{1}{3 + \frac{1}{3}}}
(A) \frac{31}{10} (B) \frac{49}{15} (C) \frac{33}{10} (D) \frac{109}{33} (E) \frac{15}{4}
- The sum of three numbers is 96. The first number is 6 times the third number, and the third number is 40 less than the second number. What is the absolute value of the difference between the first and second numbers? 三个数之和为96.第一个数是第三个数的6倍,第三个数比第二个数少40.问第一个数与第二个数之差的绝对值是多少?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
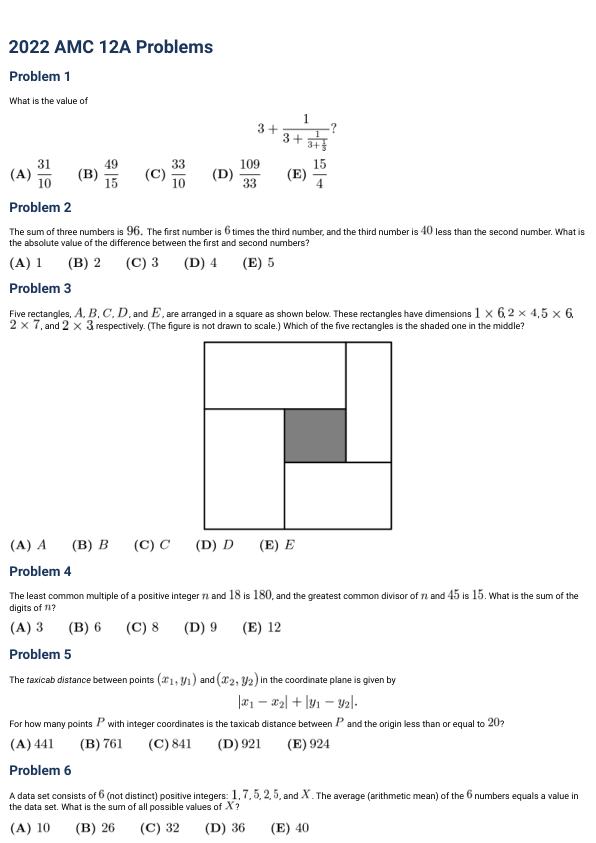
- Five rectangles, A, B, C, D, and E, are arranged in a square as shown below. These rectangles have dimensions 1×6, 2×4, 5×6, 2×7, and 2×3, respectively. (The figure is not drawn to scale.) Which of the five rectangles is the shaded one in the middle? 如下图所示,五个矩形,A、B、C、D、E,排列在一个正方形中.这些矩形的尺寸分别为1×6,2×4,5×6,2×7,2×3.(图形未按比例绘制.)问五个矩形中哪一个是中间的阴影矩形?
(A) A (B) B (C) C (D) D (E) E

英文真题
2022 AMC 12A Problems Problem 1 What is the value of $3+\frac{1}{3+\frac{1}{3+\frac13}}$?
(A) $\frac{31}{10}$ (B) $\frac{49}{15}$ (C) $\frac{33}{10}$ (D) $\frac{109}{33}$ (E) $\frac{15}{4}$
Problem 2 The sum of three numbers is $96$. The first number is $6$ times the third number, and the third number is $40$ less than the second number. What is the absolute value of the difference between the first and second numbers?
(A) $1$ (B) $2$ (C) $3$ (D) $4$ (E) $5$
Problem 3 Five rectangles, A, B, C, D, and E, are arranged in a square as shown below. These rectangles have dimensions $1\times 6$, $2\times 4$, $5\times 6$, $2\times 7$, and $2\times 3$, respectively. (The figure is not drawn to scale.) Which of the five rectangles is the shaded one in the middle?
(A) A (B) B (C) C (D) D (E) E
Problem 4 The least common multiple of a positive integer $n$ and $18$ is $180$, and the greatest common divisor of $n$ and $45$ is $15$. What is the sum of the digits of $n$?
(A) $3$ (B) $6$ (C) $8$ (D) $9$ (E) $12$
Problem 5 The taxicab distance between points $(x_1,y_1)$ and $(x_2,y_2)$ in the coordinate plane is given by
$$|x_1-x_2|+|y_1-y_2|.$$ For how many points $P$ with integer coordinates is the taxicab distance between $P$ and the origin less than or equal to $20$?
(A) $441$ (B) $761$ (C) $841$ (D) $921$ (E) $924$
Problem 6 A data set consists of $6$ (not distinct) positive integers: $1, 7, 5, 2, 5,$ and $X$. The average (arithmetic mean) of the $6$ numbers equals a value in the data set. What is the sum of all possible values of $X$?
(A) $10$ (B) $26$ (C) $32$ (D) $36$ (E) $40$
真题文字详解(英文)
Problem 1 The following problem is from both the 2022 AMC 10A #1 and 2022 AMC 12A #1, so both problems redirect to this page. What is the value of $$3+ \frac{1}{3+ \frac{1}{3+ \frac{1}{\ddots}}}$$ ? (A) $\frac{31}{10}$ (B) $\frac{49}{15}$ (C) $\frac{33}{10}$ (D) $\frac{109}{33}$ (E) $\frac{15}{4}$ Solution 1 We have $$3 + \frac{1}{3 + \frac{1}{3 + \frac{1}{\ddots}}} = 3 + \frac{1}{3 + \frac{1}{3 + \frac{1}{\left(\frac{10}{3}\right)}}} = 3 + \frac{1}{3 + \frac{1}{\left(\frac{33}{10}\right)}} = 3 + \frac{10}{33} = \boxed{\text{(D)} \frac{109}{33}}.$$ ~MRENTHUSIASM Solution 2 Continued fractions with integer parts $q_i$ and numerators all 1 can be calculated as $$\frac{[q_0, q_1, q_2, \ldots, q_n]}{[q_1, q_2, \ldots, q_n]}$$ where $$[q_0, q_1, q_2, \ldots, q_n] = q_0[q_1, q_2, \ldots, q_n] + [q_2, \ldots, q_n]$$ Solution 3 Finite continued fractions of form $n + \frac{1}{n + \frac{1}{n + \cdots}} = \frac{x}{y}$ have linear combinations of $x$, $y$ that solve Pell's Equation. Specifically, the denominator $y$ and numerator $x$ are solutions to the Diophantine equation $(n^2 + 4)\left(\frac{y}{2}\right)^2 - \left(x - \frac{ny}{2}\right)^2 = \pm 1$. So for this problem in particular, the denominator $y$ and numerator $x$ are solutions to the Diophantine equation $13\left(\frac{y}{2}\right)^2 - \left(x - \frac{3y}{2}\right)^2 = \pm 1$. That leaves two answers. Since the number of 1's in the continued fraction is odd, we further narrow it down to $13\left(\frac{y}{2}\right)^2 - \left(x - \frac{3y}{2}\right)^2 = -1$, which only leaves us with 1 answer and that is $(x, y) = (109, 33)$ which means $\boxed{\text{(D)} \frac{109}{33}}.$ (Note: Integer solutions increase exponentially, so our next solution will have a numerator greater than $3^2(109)$. Therefore, when you don't see numerators greater than $3^2(109)$ in the answer choices, this method should be fine.)

真题文字详解(中英双语)
Problem 1 The following problem is from both the 2022 AMC 10A #1 and 2022 AMC 12A #1, so both problems redirect to this page. 以下问题既来自2022年AMC 10A第1题,也来自2022年AMC 12A第1题,因此这两个问题都指向这一页。
What is the value of $$3+ \frac{1}{3+\frac{1}{3+\frac13}}$$ ?
(A) ( \frac{31}{10} )
(B) ( \frac{49}{15} )
(C) ( \frac{33}{10} )
(D) ( \frac{109}{33} )
(E) ( \frac{15}{4} )
Solution 1 We have
$$3 + \frac{1}{3 + \frac{1}{3 + \frac{1}{3}}} = 3 + \frac{1}{3 + \frac{1}{\left(3 + \frac{1}{3}\right)}} = 3 + \frac{1}{3 + \frac{3}{10}} = 3 + \frac{1}{\left(\frac{39}{10}\right)} = 3 + \frac{10}{33} = \boxed{\text{(D)} \frac{109}{33}}.$$
~MRENTHUSIASM 我们有 ~MRENTHUSIASM
Solution 2 Continued fractions with integer parts ( q_i ) and numerators all 1 can be calculated as
$$\frac{[q_0, q_1, q_2, \ldots, q_n]}{[q_1, q_2, \ldots, q_n]},$$
where
分数部分为( q_i ),分子全为1的连分式可以计算为,其中
$$\begin{aligned}
& [q_0, q_1, q_2, \ldots, q_n] = q_0[q_1, q_2, \ldots, q_n] + [q_2, \ldots, q_n]
\end{aligned}$$
Solution 3

