2013 澳洲 AMC D-Intermediate 真题 答案 详解
2013-10-09 auamc auamc D-Intermediate
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2013-D-Intermediate-paper-eng-zh.pdf | 6 页 | 240.82KB | 中英双语真题 |
| 2 | 2013-D-Intermediate-paper-eng.pdf | 6 页 | 57.09KB | 英文真题 |
| 3 | 2013-D-Intermediate-key.pdf | 1 页 | 11.61KB | 真题答案 |
| 4 | 2013-D-Intermediate-solution-eng.pdf | 10 页 | 368.34KB | 真题文字详解(英文) |
中英双语真题
Intermediate Paper
1-10 questions, 3 points each
-
The expression (2013 + 2014 + 2015) equals
(A) 642 (B) 2016 (C) 6022 (D) 6032 (E) 6042 -
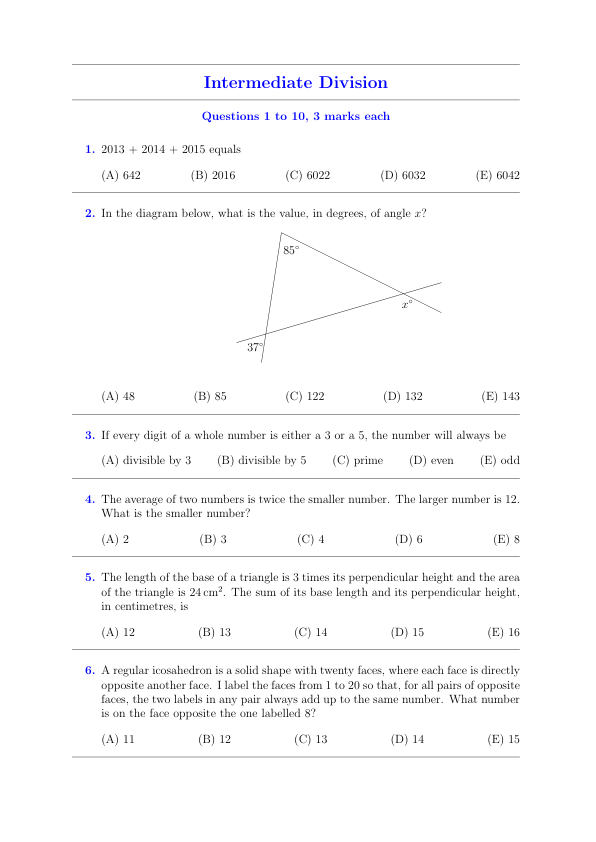
In the diagram below, what is the value of (x)?
(A) 48 (B) 85 (C) 122 (D) 132 (E) 143 -
If a positive integer's digits can only be 3 or 5, which statement about this number is always true?
(A) Divisible by 3 (B) Divisible by 5 (C) Prime (D) Even (E) Odd -
Given that the average of two numbers is twice the smaller number, if the larger number is 12, what is the smaller number?
(A) 2 (B) 3 (C) 4 (D) 6 (E) 8 -
A triangle with a base three times its height has an area of 24 cm². What is the sum of its base and height?
(A) 12 (B) 13 (C) 14 (D) 15 (E) 16 -
A regular twenty-sided solid is a polyhedron with twenty faces, where every face is congruent to another. Each face is labeled with a number from 1 to 20 such that the sum of numbers on opposite faces is equal. What is the number on the face opposite the one labeled 8?
(A) 11 (B) 12 (C) 13 (D) 14 (E) 15 -
If (p = 4b^2 + 26) and (b) is a positive integer, then (p) cannot be divisible by:
(A) 2 (B) 4 (C) 5 (D) 6 (E) 7

英文真题
Intermediate Division
Questions 1 to 10, 3 marks each
-
(2013 + 2014 + 2015) equals
(A) 642
(B) 2016
(C) 6022
(D) 6032
(E) 6042 -
In the diagram below, what is the value, in degrees, of angle (x)?
(A) 48
(B) 85
(C) 122
(D) 132
(E) 143 -
If every digit of a whole number is either a 3 or a 5, the number will always be
(A) divisible by 3
(B) divisible by 5
(C) prime
(D) even
(E) odd -
The average of two numbers is twice the smaller number. The larger number is 12. What is the smaller number?
(A) 2
(B) 3
(C) 4
(D) 6
(E) 8 -
The length of the base of a triangle is 3 times its perpendicular height and the area of the triangle is (24 \text{ cm}^2). The sum of its base length and its perpendicular height, in centimetres, is
(A) 12
(B) 13
(C) 14
(D) 15
(E) 16 -
A regular icosahedron is a solid shape with twenty faces, where each face is directly opposite another face. I label the faces from 1 to 20 so that, for all pairs of opposite faces, the two labels in any pair always add up to the same number. What number is on the face opposite the one labelled 8?
(A) 11
(B) 12
(C) 13
(D) 14
(E) 15
真题文字详解(英文)
SOLUTIONS - INTERMEDIATE DIVISION 1. 2013 + 2014 + 2015 = 6042, hence (E). 2. Angle x° is the sum of the two opposite interior angles, so x = 85 + 37 = 122, hence (C). 3. (Also J7) If every digit of a whole number is either a 3 or a 5, the number must be odd. Note that 33 is not prime, even or divisible by 5 and 35 is not divisible by 3, showing that odd is the only consistent descriptor, hence (E). 4. Let x be the smaller number. Then (\frac{x+12}{2} = 2x \rightarrow x+12=4x \rightarrow 12=3x \rightarrow x=4), hence (C). 5. For any triangle, (A=\frac{1}{2}bh). Here b = 3h, so A = 24 = (\frac{3}{2}h^2 \rightarrow 3h^2 = 48 \rightarrow h^2 = 16 \rightarrow h = 4). Thus base + height = 4+12 = 16 centimetres, hence (E). 6. Each pair of opposite faces adds to 21 and 8 + 13 = 21, hence (C). 7. (Also S5) When b = 1, p = 30 (which is divisible by 2, 5 and 6). When b = 4, p = 42 (which is divisible by 7). This eliminates alternatives A, C, D and E. However, 4p + 26 = 4(p + 6) + 2 so p cannot be divisible by 4, hence (B). 8. The faster dog runs 100 m while the slower dog runs 50 m, so the latter is still 20 m away when the former reaches me, hence (B). 9. If (x=\frac{2}{3}), then (x^2=\frac{4}{9}) and (\frac{1}{x^2}=\frac{9}{4}). Adding, we obtain (\frac{9}{4}+\frac{4}{9}=\frac{97}{36}=2\frac{25}{36}), which is between 2.5 and 3, hence (D).

