2017 澳洲 AMC C-Junior 真题 答案 详解
2017-10-09 auamc auamc C-Junior
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2017-C-Junior-paper-eng-zh.pdf | 9 页 | 277.87KB | 中英双语真题 |
| 2 | 2017-C-Junior-paper-eng.pdf | 6 页 | 55.20KB | 英文真题 |
| 3 | 2017-C-Junior-key.pdf | 1 页 | 25.09KB | 真题答案 |
| 4 | 2017-C-Junior-solution-eng.pdf | 8 页 | 1.48MB | 真题文字详解(英文) |
中英双语真题
1-10 Questions, 3 marks each
Questions 1 to 10, 3 marks each
-
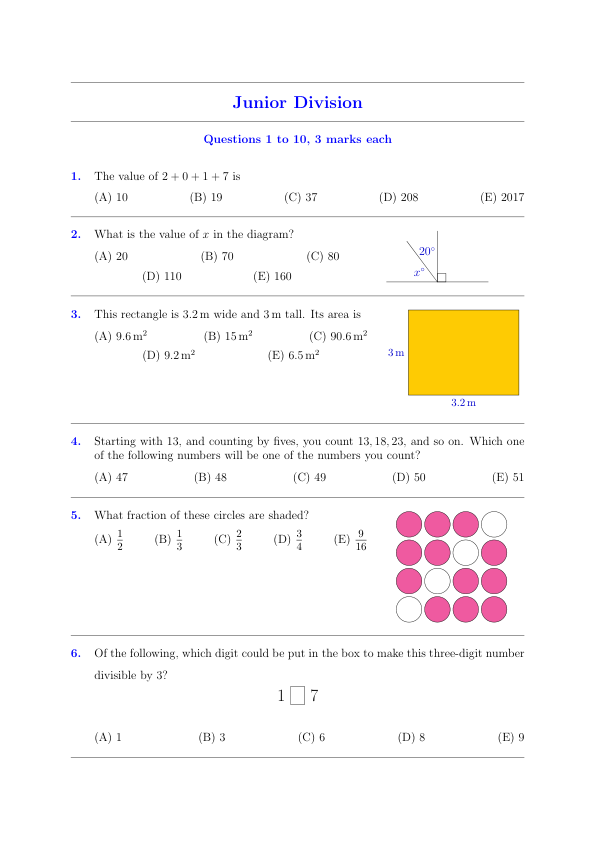
算式2+0+1+7之值等于 The value of 2 + 0 + 1 + 7 is
(A) 10 (B) 19 (C) 37 (D) 208 (E) 2017 -
在右图中,请问x之值是什么? What is the value of x in the diagram?
(A) 20 (B) 70 (C) 80 (D) 110 (E) 160 -
在右图中,矩形的长为3.2m、宽为3m。则这个矩形的面积等于 This rectangle is 3.2 m wide and 3 m tall. Its area is
(A) 9.6 m² (B) 15 m² (C) 90.6 m² (D) 9.2 m² (E) 6.5 m² -
从13开始数起,接着每个数都增加5,所数出的数为13、18、23…。请问下列哪一选项之中的数是您将会数出的数之一? Starting with 13, and counting by fives, you count 13, 18, 23, and so on. Which one of the following numbers will be one of the numbers you count?
(A) 47 (B) 48 (C) 49 (D) 50 (E) 51 -
请问图中有几分之几的圆圈被涂上阴影? What fraction of these circles are shaded?
(A) ( \frac{1}{2} ) (B) ( \frac{1}{3} ) (C) ( \frac{2}{3} ) (D) ( \frac{3}{4} ) (E) ( \frac{9}{16} )

英文真题
Junior Division
Questions 1 to 10, 3 marks each
-
The value of (2 + 0 + 1 + 7) is
(A) 10
(B) 19
(C) 37
(D) 208
(E) 2017 -
What is the value of (x) in the diagram?
(A) 20
(B) 70
(C) 80
(D) 110
(E) 160 -
This rectangle is 3.2 m wide and 3 m tall. Its area is
(A) 9.6 m²
(B) 15 m²
(C) 90.6 m²
(D) 9.2 m²
(E) 6.5 m² -
Starting with 13, and counting by fives, you count 13, 18, 23, and so on. Which one of the following numbers will be one of the numbers you count?
(A) 47
(B) 48
(C) 49
(D) 50
(E) 51 -
What fraction of these circles are shaded?
(A) (\frac{1}{2})
(B) (\frac{1}{3})
(C) (\frac{2}{3})
(D) (\frac{3}{4})
(E) (\frac{9}{16}) -
Of the following, which digit could be put in the box to make this three-digit number divisible by 3?
(1 \square 7)
(A) 1
(B) 3
(C) 6
(D) 8
(E) 9
真题文字详解(英文)
Solutions - Junior Division
1. (Also MP1) 2 + 0 + 1 + 7 = 10, hence (A).
2. The two angles on the left form a right angle: 20° + x° = 90°. Then x° = 90° - 20° = 70°, hence (B).
3. The area is 3 × 3.2 = 9.6 m², hence (A).
4. The numbers counted are those that are 3 more than a multiple of 5. The units digit of this sequence alternates between 3 and 8. Of the answers given, only 48 has one of these units digits, hence (B).
5. In each row of 4 circles, 3 are shaded, so that (\frac{3}{4}) of the circles are shaded, hence (D).
6. A number is divisible by 3 when the sum of its digits is a multiple of 3. The known digits add to 1 + 7 = 8, which is 1 less than a multiple of 3. So the unknown digit will be 1 more than a multiple of 3, either 1, 4 or 7. Of these, only 1 is listed, hence (A).
7. With 32 litres, it will run 4 times longer than with 8 litres. This is 4 × 150 = 600 minutes = 10 hours, hence (D).
8. In kilograms, 0.15 + 0.78 + 1.35 + 0.68 = 2.96, hence (D).
9. (Also I4, S3) 100% of 1 is 1, and 1000% is 10 times greater, which is 10, hence (C).
10. For the fraction to be between (7 = \frac{42}{6}) and (8 = \frac{48}{6}), the numerator must be between 42 and 48. For this, the number in the box must be between 39 and 45. Of the five numbers given, only 41 is in this range, hence (E).

