2017 澳洲 AMC D-Intermediate 真题 答案 详解
2017-10-08 auamc auamc D-Intermediate
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2017-D-Intermediate-paper-eng-zh.pdf | 19 页 | 520.51KB | 中英双语真题 |
| 2 | 2017-D-Intermediate-paper-eng.pdf | 6 页 | 58.99KB | 英文真题 |
| 3 | 2017-D-Intermediate-key.pdf | 1 页 | 25.09KB | 真题答案 |
| 4 | 2017-D-Intermediate-solution-eng.pdf | 10 页 | 2.04MB | 真题文字详解(英文) |
中英双语真题
1-10 Questions, 3 marks each
1. 将2017除以5所得的余数为
The remainder when 2017 is divided by 5 is
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
-
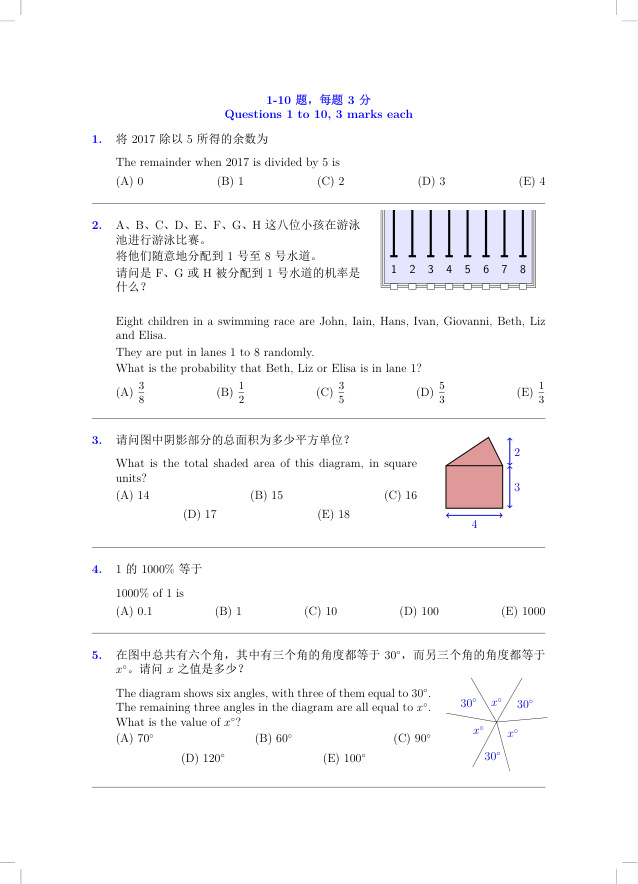
A、B、C、D、E、F、G、H 这八位小孩在游泳池进行游泳比赛。
将他们随意地分配到1号至8号水道。
请问是 F、G 或 H 被分配到1号水道的机率是什么?
Eight children in a swimming race are John, Iain, Hans, Ivan, Giovanni, Beth, Liz and Elisa.
They are put in lanes 1 to 8 randomly.
What is the probability that Beth, Liz or Elisa is in lane 1?
(A) ( \frac{3}{8} ) (B) ( \frac{1}{2} ) (C) ( \frac{3}{5} ) (D) ( \frac{5}{3} ) (E) ( \frac{1}{3} ) -
请问图中阴影部分的总面积为多少平方单位?
What is the total shaded area of this diagram, in square units?
(A) 14 (B) 15 (C) 16 (D) 17 (E) 18 -
1 的1000%等于
1000% of 1 is
(A) 0.1 (B) 1 (C) 10 (D) 100 (E) 1000 -
在图中总共有六个角,其中有三个角的度数都等于30°,而另三个角的度数都等于x°。请问x之值是多少?
The diagram shows six angles, with three of them equal to 30°. The remaining three angles in the diagram are all equal to x°. What is the value of x°?
(A) 70° (B) 60° (C) 90° (D) 120° (E) 100°
英文真题
Intermediate Division
Questions 1 to 10, 3 marks each
-
The remainder when 2017 is divided by 5 is
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4 -
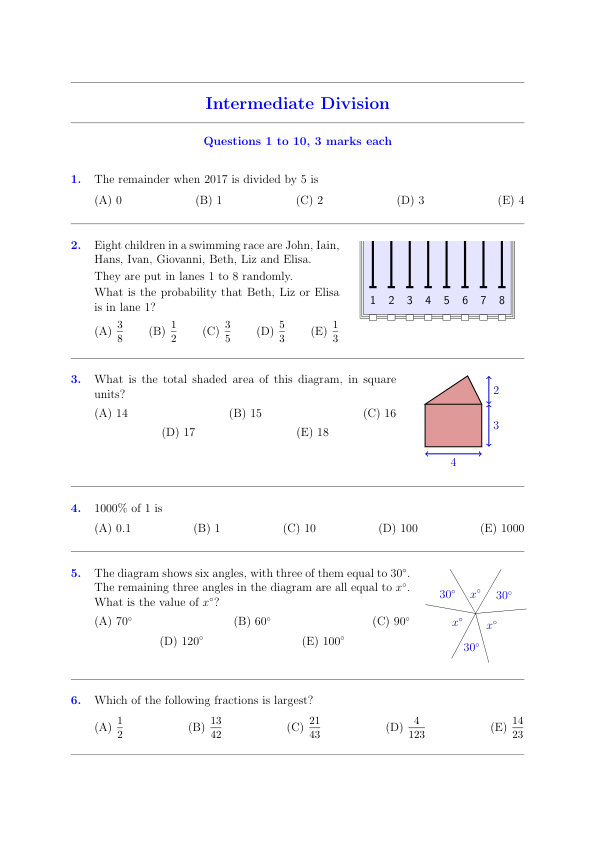
Eight children in a swimming race are John, Iain, Hans, Ivan, Giovanni, Beth, Liz and Elisa. They are put in lanes 1 to 8 randomly. What is the probability that Beth, Liz or Elisa is in lane 1?
(A) ( \frac{3}{8} )
(B) ( \frac{1}{2} )
(C) ( \frac{3}{5} )
(D) ( \frac{5}{3} )
(E) ( \frac{1}{3} ) -
What is the total shaded area of this diagram, in square units?
(A) 14
(B) 15
(C) 16
(D) 17
(E) 18 -
1000% of 1 is
(A) 0.1
(B) 1
(C) 10
(D) 100
(E) 1000 -
The diagram shows six angles, with three of them equal to 30°. The remaining three angles in the diagram are all equal to x°. What is the value of x°?
(A) 70°
(B) 60°
(C) 90°
(D) 120°
(E) 100° -
Which of the following fractions is largest?
(A) ( \frac{1}{2} )
(B) ( \frac{13}{42} )
(C) ( \frac{21}{43} )
(D) ( \frac{4}{123} )
(E) ( \frac{14}{23} )
真题文字详解(英文)
Solutions – Intermediate Division 1. The number 2015 is a multiple of 5, so the remainder is 2, hence (C). 2. (Also S1) Each of the 8 children is equally likely to be in lane 1, so the probability that one of the three identified students is in lane 1 is (\frac{3}{8}); hence (A). 3. The rectangle has area (3 \times 4 = 12) and the triangle has area (\frac{1}{2} \times 4 \times 2 = 4). The total area is (12 + 4 = 16), hence (C). 4. (Also J9, S3) 100% of 1 is 1, and 1000% is 10 times greater, which is 10, hence (C). 5. The angles around the point add to 360°. So (3x + 90 = 360), which means that (3x = 270) and (x = 90), hence (C). 6. Using (\frac{1}{2}) as a test, only (\frac{14}{23}) is larger, hence (E). 7. (Also J11, S6) There are many ways to solve this with 4 swaps. For example, WORDS → WORSD → WOSRD → WSORD → SWORD This suggests that the answer is 4. Suppose this isn’t the smallest: some solution with three or fewer swaps changes WORDS to SWORD. Each swap involves two letters, and each letter must be swapped at least once. When swapping five objects with these conditions, the only pattern of swaps possible is shown in the diagram: there are three swaps, one object is swapped twice and all other objects are swapped only once. In particular, there is a pair of objects that are swapped only with each other. Such a pattern of swaps can't transform WORDS into SWORD, since there is no pair of letters which have only been swapped with each other. Consequently the smallest possible number of swaps is 4, hence (B). 48 2017 AMC — Intermediate Solutions

