2020 澳洲 AMC D-Intermediate 真题 答案 详解
2020-10-10 auamc auamc D-Intermediate
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2020-D-Intermediate-paper-eng-zh.pdf | 10 页 | 1.31MB | 中英双语真题 |
| 2 | 2020-D-Intermediate-paper-eng.pdf | 6 页 | 347.32KB | 英文真题 |
| 3 | 2020-D-Intermediate-key.pdf | 1 页 | 40.38KB | 真题答案 |
| 4 | 2020-D-Intermediate-solution-eng.pdf | 9 页 | 2.04MB | 真题文字详解(英文) |
中英双语真题
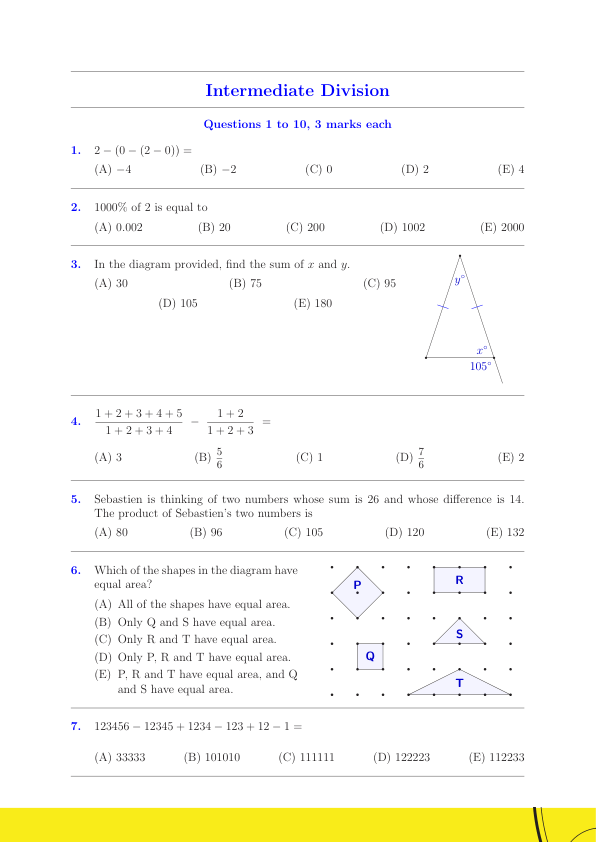
2020 Australian Mathematics Competition – Intermediate 1-10 题,每题3分 Questions 1 to 10, 3 marks each 1. 计算 $2 - (0 - (2 - 0)) = $
$2 - (0 - (2 - 0)) = $
(A) -4 (B) -2 (C) 0 (D) 2 (E) 4 2. 请问 2 的 1000% 等于多少?
1000% of 2 is equal to
(A) 0.002 (B) 20 (C) 200 (D) 1002 (E) 2000 3. 在右图中,请问 x 与 y 之和等于多少?
In the diagram provided, find the sum of x and y.
(A) 30 (B) 75 (C) 95 (D) 105 (E) 180 4. 计算 $\frac{1 + 2 + 3 + 4 + 5}{1 + 2 + 3 + 4} - \frac{1 + 2}{1 + 2 + 3} = $
$\frac{1 + 2 + 3 + 4 + 5}{1 + 2 + 3 + 4} - \frac{1 + 2}{1 + 2 + 3} = $
(A) 3 (B) $\frac{5}{6}$ (C) 1 (D) $\frac{7}{6}$ (E) 2 5. 小莎心里想着两个数,它们的和为 26、差为 14。请问小莎想的这两个数的乘积是多少?
Sebastien is thinking of two numbers whose sum is 26 and whose difference is 14. The product of Sebastien's two numbers is
(A) 80 (B) 96 (C) 105 (D) 120 (E) 132

英文真题
Intermediate Division
Questions 1 to 10, 3 marks each
-
$2 - (0 - (2 - 0)) = $
(A) -4
(B) -2
(C) 0
(D) 2
(E) 4 -
1000% of 2 is equal to
(A) 0.002
(B) 20
(C) 200
(D) 1002
(E) 2000 -
In the diagram provided, find the sum of x and y.
(A) 30
(B) 75
(C) 95
(D) 105
(E) 180 -
$\frac{1 + 2 + 3 + 4 + 5}{1 + 2 + 3 + 4} - \frac{1 + 2}{1 + 2 + 3} = $
(A) 3
(B) $\frac{5}{6}$
(C) 1
(D) $\frac{7}{6}$
(E) 2 -
Sebastien is thinking of two numbers whose sum is 26 and whose difference is 14. The product of Sebastien's two numbers is
(A) 80
(B) 96
(C) 105
(D) 120
(E) 132 -
Which of the shapes in the diagram have equal area?
(A) All of the shapes have equal area.
(B) Only Q and S have equal area.
(C) Only R and T have equal area.
(D) Only P, R and T have equal area.
(E) P, R and T have equal area, and Q and S have equal area. -
$123456 - 12345 + 1234 - 123 + 12 - 1 = $
(A) 33333
(B) 101010
(C) 111111
(D) 122223
(E) 112233
真题文字详解(英文)
2020 AMC Intermediate Solutions 63 Intermediate Solutions 1. (Also J6) 2 - (0 - (2 - 0)) = 2 - (0 - 2) = 2 - (-2) = 2 + 2 = 4, hence (E). 2. 1000% of 2 = \frac{1000}{100} \times 2 = 10 \times 2 = 20, hence (B). 3. (Also S2) The supplementary angle to 105° is x = 75. Since the triangle is isosceles, the other base angle is 75° and the apex angle is y = 180 - 2 \times 75 = 30. Then x + y = 75 + 30 = 105, hence (D). 4. (Also J9) \frac{1+2+3+4+5}{1+2+3+4} - \frac{1+2}{1+2+3} = \frac{15}{10} - \frac{3}{6} = \frac{3}{2} - \frac{1}{2} = 1, hence (C). 5. (Also J10, S4) Alternative 1 The average of the two numbers is 26 ÷ 2 = 13, so that they are equal distances above and below 13. Since they differ by 14, the distance above and below 13 is 14 ÷ 2 = 7. That is, the two numbers are 13 - 7 = 6 and 13 + 7 = 20, and their product is 6 × 20 = 120, hence (D). Alternative 2 Let the smaller number be x, so that the larger is 14 + x. Then x + (14 + x) = 26, giving 2x = 26 - 14 = 12, and so x = 6. Therefore, the numbers are 6 and 20, with product 6 × 20 = 120, hence (D). 6. In grid squares, Q has area 1 and R has area 2. Shape S can be cut into two triangles that rearrange to cover Q, so S has area 1. Shape P has twice the area of S, so P has area 2. Finally, T can be cut into two right-angled triangles that rearrange to cover R, so that T has area 2. Then in grid squares, P = R = T = 2 and Q = S = 1, hence (E). 7. (Also J12) (123456 - 12345) + (1234 - 123) + (12 - 1) = 111111 + 1111 + 11 = 112233, hence (E). www.amt.edu.au

