2022 澳洲 AMC E-Senior 真题 答案 详解
2022-10-07 auamc auamc E-Senior
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2022-E-Senior-paper-eng-zh.pdf | 6 页 | 355.23KB | 中英双语真题 |
| 2 | 2022-E-Senior-paper-eng.pdf | 6 页 | 145.91KB | 英文真题 |
| 3 | 2022-E-Senior-key.pdf | 1 页 | 14.91KB | 真题答案 |
| 4 | 2022-E-Senior-solution-eng.pdf | 10 页 | 140.79KB | 真题文字详解(英文) |
中英双语真题
Senior Questions
1-10 questions, 3 points each
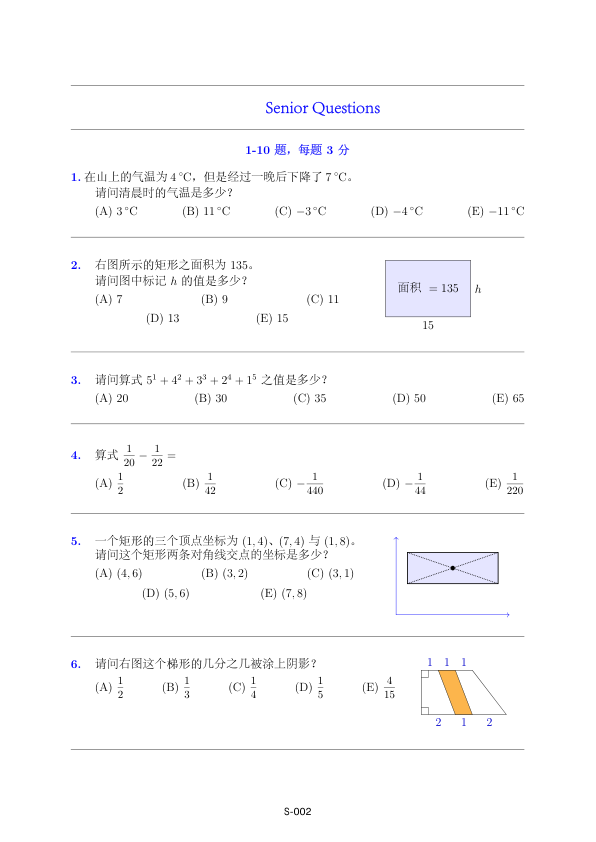
1. The temperature on the mountain was 4°C, but after a night it dropped by 7°C. What was the temperature at dawn?
(A) 3°C (B) 11°C (C) -3°C (D) -4°C (E) -11°C
-
The area of the rectangle shown in the diagram is 135. What is the value of h?
(A) 7 (B) 9 (C) 11 (D) 13 (E) 15 -
Calculate the value of (5^1 + 4^2 + 3^3 + 2^4 + 1^5).
(A) 20 (B) 30 (C) 35 (D) 50 (E) 65 -
Simplify (\frac{1}{20} - \frac{1}{22}).
(A) (\frac{1}{2}) (B) (\frac{1}{42}) (C) (-\frac{1}{440}) (D) (-\frac{1}{44}) (E) (\frac{1}{220}) -
A rectangle has three vertices with coordinates (1,4), (7,4), and (1,8). What are the coordinates of the intersection point of its diagonals?
(A) (4,6) (B) (3,2) (C) (3,1) (D) (5,6) (E) (7,8) -
What fraction of the trapezoid in the diagram is shaded?
(A) (\frac{1}{2}) (B) (\frac{1}{3}) (C) (\frac{1}{4}) (D) (\frac{1}{5}) (E) (\frac{4}{15})
英文真题
2022 AMC Senior Questions 27 Senior Questions 1. The temperature in the mountains was 4°C but dropped overnight by 7°C. What was the temperature in the morning? (A) 3°C (B) 11°C (C) -3°C (D) -4°C (E) -11°C 2. The rectangle shown has area 135. What is the value of h in the diagram? (A) 7 (B) 9 (C) 11 (D) 13 (E) 15 Area = 135 h 15 3. The value of 5^1 + 4^2 + 3^3 + 2^4 + 1^5 is (A) 20 (B) 30 (C) 35 (D) 50 (E) 65 4. \frac{1}{20} - \frac{1}{22} = (A) \frac{1}{2} (B) \frac{1}{42} (C) -\frac{1}{440} (D) -\frac{1}{44} (E) \frac{1}{220} 5. Three vertices of a rectangle are the points (1, 4), (7, 4) and (1, 8). At which point do the diagonals of the rect- angle cross? (A) (4,6) (B) (3,2) (C) (3,1) (D) (5,6) (E) (7,8) 6. What fraction of this trapezium is shaded? (A) \frac{1}{2} (B) \frac{1}{3} (C) \frac{1}{4} (D) \frac{1}{5} (E) \frac{4}{15} 7. The sum of the numbers on these six cards is 4√5. Lily removes one of them. What is the largest possible sum of the re- maining five cards? (A) 4√5 + 3√7 (B) 4√5 + 7√7 (C) 4√5 - 2√7 (D) 4√5 - 5√7 (E) 4√5 + 4√7 www.amt.edu.au

真题文字详解(英文)
64 2022 AMC Senior Solutions Senior Solutions 1. (Also J2) 4 - 7 = -3, hence (C). 2. 135 ÷ 15 = 9, hence (B). 3. 5^1 + 4^2 + 3^3 + 2^4 + 1^5 = 5 + 16 + 27 + 16 + 1 = 65, hence (E). 4. \frac{1}{20} - \frac{1}{22} = \frac{11}{220} - \frac{10}{220} = \frac{1}{220}, hence (E). 5. (Also I11) The diagonals of the rectangle meet at the midpoints of its two diagonals. One of these diagonals has endpoints (1,8) and (7,4). The midpoint is found by averaging coordinates (\frac{1+7}{2}, \frac{8+4}{2}) = (4,6), hence (A). 6. Alternative 1 Let the perpendicular height of the trapezium (and hence the shaded parallelogram) be h. Then the area of the large trapezium is \frac{1}{2}(3+5)h = 4h and the area of the shaded parallelogram is 1h = h. So \frac{1}{4} of the area is shaded, hence (C). Alternative 2 In this grid of five rectangles, the trapezium is shaded. Since the last two rectangles are together half shaded, the trapezium's area is 4 grid rectangles. The area coloured gold is two half grid grid rectangles, for a total of 1 grid rectangle. So this is \frac{1}{4} of the trapezium's area, hence (C). 7. To leave the largest possible sum, we need to remove the smallest number. This will be the most negative number which is -4\sqrt{7}. The sum of the remaining five numbers is (1+3)\sqrt{5} + (2+5-3)\sqrt{7} = 4\sqrt{5} + 4\sqrt{7}, hence (E). 8. The angle sum in a quadrilateral is 360°. Thus 140 + 90 + 2x = 360 and so 2x = 130 and x = 65, hence (A). www.amt.edu.au

