2017 DSE 数学延伸部分-M2 真题 答案 详解
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2017-数学延伸部分-M2-paper-eng.pdf | 28 页 | 4.68MB | 真题(英文) |
| 2 | 2017-数学延伸部分-M2-paper-zh.pdf | 28 页 | 5.73MB | 真题(中文) |
| 3 | 2017-数学延伸部分-M2-answer-zh.pdf | 14 页 | 2.32MB | 答案(中文) |
| 4 | 2017-数学延伸部分-M2-answer-eng.pdf | 13 页 | 2.69MB | 答案(英文) |
真题(英文)
2017-DSE MATH EP M2
HONG KONG EXAMINATIONS AND ASSESSMENT AUTHORITY HONG KONG DIPLOMA OF SECONDARY EDUCATION EXAMINATION 2017
MATHEMATICS Extended Part Module 2 (Algebra and Calculus) Question-Answer Book
8:30 am - 11:00 am (2½ hours)
This paper must be answered in English
INSTRUCTIONS
(1) After the announcement of the start of the examination, you should first write your Candidate Number in the space provided on Page 1 and stick barcode labels in the spaces provided on Pages 1, 3, 5, 7, 9, 11 and 13.
(2) This paper consists of TWO sections, A and B.
(3) Attempt ALL questions in this paper. Write your answers in the spaces provided in this Question-Answer Book. Do not write in the margins. Answers written in the margins will not be marked.
(4) Graph paper and supplementary answer sheets will be supplied on request. Write your Candidate Number, mark the question number box and stick a barcode label on each sheet, and fasten them with string INSIDE this book.
(5) Unless otherwise specified, all working must be clearly shown.
(6) Unless otherwise specified, numerical answers must be exact.
(7) No extra time will be given to candidates for sticking on the barcode labels or filling in the question number boxes after the 'Time is up' announcement.
© Hong Kong Examinations and Assessment Authority All Rights Reserved 2017
2017-DSE-MATH-EP(M2)-1 28
Please stick the barcode label here
Candidate Number
- A 032E001 Provided by dse.life

真题(中文)
2017-DSE 數學 延伸部分 單元二
香港考試及評核局 2017年香港中學文憑考試
數學 延伸部分 單元二(代數與微積分) 試題答題簿
本試卷必須用中文作答 兩小時三十分鐘完卷 (上午八時三十分至上午十一時)
考生须知 (一) 宣布開考後,考生須首先在第1頁之適當位置填寫考生編號,並在第1、3、5、7、9、11及13頁之適當位置貼上電腦條碼。 (二) 本試卷分兩部,即甲部和乙部。 (三) 本試卷各題均須作答,答案須寫在本試題答題簿中预留的空位內。不可在各頁邊界以外位置書寫。寫於邊界以外的答案,將不予評閱。 (四) 如有需要,可要求派發方格紙及補充答题紙。每張紙均須填寫考生編號、填畫試題編號方格、貼上電腦條碼,並用繩綁於簿內。 (五) 除特別指明外,須詳細列出所有算式。 (六) 除特別指明外,數值答案須用真確值表示。 (七) 試場主任宣布停筆後,考生不會獲得額外時間貼上電腦條碼及填畫試題編號方格。
©香港考試及評核局保留版權 Hong Kong Examinations and Assessment Authority All Rights Reserved 2017
2017-DSE-MATH-EP(M2)-1 28
請在此貼上電腦條碼 考生編號
更多试卷歡迎瀏覽http://dsepp.com

答案(中文)
評卷參考 單元二(代數與微積分)
本文件供閱卷員參考而設,並不應被視為標準答案。考生以及沒有參與評卷工作的教師在論文內容時應小心謹慎。
一般閱卷原則
-
評卷時,閱卷員須跟循評卷參考的部分標準給分,這是十分重要的。很多時考生會運用評卷參考以外的方 法而得到正確答案,一般來說,只要運用合理的方法而取得正確答案,該考生可獲得該部分的所有分数(除題目特別指明方法外)。閱卷員應有耐性地評閱評卷參考以外的解題方法。
-
在評卷參考中,分數會分為下列三類: 「M」分 使用正確方法的得分; 「A」分 正確答案的得分; 沒有「M」或「A」的分 正確地完成證題或推演得題目所給的答案的得分。 某些題目由數部分組成,而較後部分的答案卻需依賴較前部分所得的结果。在這情况下, 若考生因為前部分錯誤的結果而導致後部分的答案錯誤,但卻能運用正確的方法去解题, 則方法正確的步驟可給「M」分,而相應的答案將沒有「A」分(除特别指明外)。
-
為方便閱卷員評卷,評卷參考已盡量詳盡。當然,考生的答案多不會如評卷參考般清楚列 寫出來,諸如欠缺某個步驟或將步驟隱含於字裏行間。如遇到類似情況,閱卷員應運用他們的專業知識去判斷是否給分。一般來說,如考生的答案顯示他已運用相關的概念或技巧,則該部分應予給分。
-
評卷時遇有不清楚的地方,應以考生的利益為依歸。
-
評卷參考中,塗上陰影的部分代表可省略的步驟,有外框的部分代表運用不同方法的答 案。所有分數答案必須化簡。
-
除在題目中特别指明外,不以真確值表示的數值答案均不被接受。
66 更多試卷歡迎瀏覽http://dsepp.com

答案(英文)
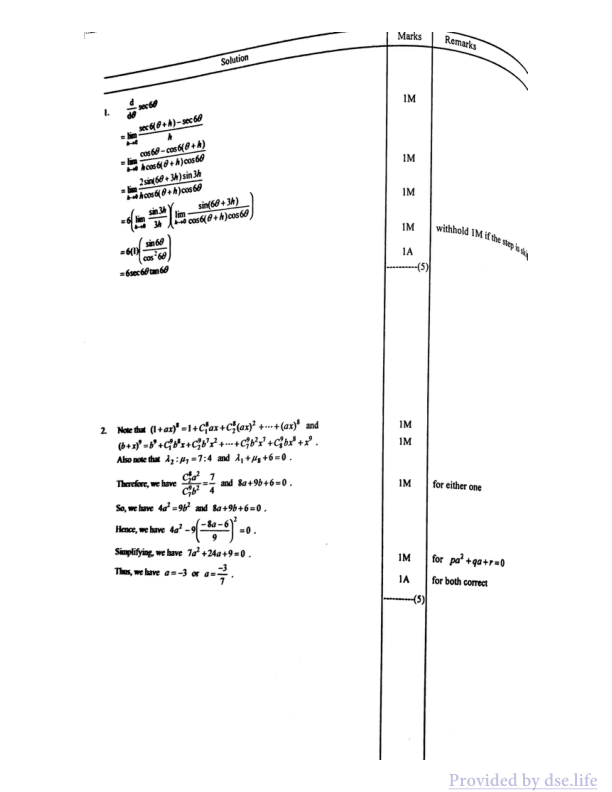
- (\frac{d}{d\theta} \sec 6\theta)
[ = \lim_{{h \to 0}} \frac{\sec 6(\theta + h) - \sec 6\theta}{h} ]
[ = \lim_{{h \to 0}} \frac{\cos 6\theta - \cos 6(\theta + h)}{h \cos 6(\theta + h) \cos 6\theta} ]
[ = \lim_{{h \to 0}} \frac{2 \sin (\theta + 3h) \sin 3h}{h \cos 6(\theta + h) \cos 6\theta} ]
[ = 6 \left( \lim_{{h \to 0}} \frac{\sin 3h}{3h} \right) \left( \lim_{{h \to 0}} \frac{\sin (6\theta + 3h)}{\cos 6(\theta + h) \cos 6\theta} \right) ]
[ = 6(1) \left( \frac{\sin 6\theta}{\cos^2 6\theta} \right) ]
[ = 6 \sec 6\theta \tan 6\theta ]
- Note that ( (1+ax)^8 = 1 + C_1^8 ax + C_2^8 (ax)^2 + ... + (ax)^8 ) and ( (b+x)^9 = b^9 + C_1^9 b^8 x + C_2^9 b^7 x^2 + ... + C_8^9 bx^8 + x^9 ). Also note that ( \lambda_2 : \mu_1 = 7:4 ) and ( \lambda_1 + \mu_8 + 6 = 0 ).
Therefore, we have ( \frac{C_2^8 a^2}{C_7^9 b^2} = \frac{7}{4} ) and ( 8a + 9b + 6 = 0 ).
So, we have ( 4a^2 = 9b^2 ) and ( 8a + 9b + 6 = 0 ).
Hence, we have ( 4a^2 - 9 \left( \frac{-8a - 6}{9} \right)^2 = 0 ).
Simplifying, we have ( 7a^2 + 24a + 9 = 0 ).
Thus, we have ( a = -3 ) or ( a = -\frac{3}{7} ).
Marks | Remarks |-------|----------------------------------------------| | 1M | withhold 1M if the step is skipped | | 1M | for either one | | 1A | for both correct |
Provided by dse.life