2018 DSE 数学延伸部分-M1 真题 答案 详解
| 序号 | 文件列表 | 说明 | ||
|---|---|---|---|---|
| 1 | 2018-数学延伸部分-M1-paper-eng.pdf | 12 页 | 3.05MB | 真题(英文) |
| 2 | 2018-数学延伸部分-M1-paper-zh.pdf | 12 页 | 4.46MB | 真题(中文) |
| 3 | 2018-数学延伸部分-M1-answer-eng.pdf | 12 页 | 2.34MB | 答案(英文) |
真题(英文)
SECTION A (50 marks)
- Let (A) and (B) be two events. Suppose that (P(A)=0.8), (P(B|A)=0.45) and (P(B|A')=0.6), where (A') is the complementary event of (A). Find
(a) (P(B)),
(b) (P(A|B)),
(c) (P(A \cup B)).
(5 marks)
Provided by dse.life

真题(中文)
甲部(50分)
- 設 ( A ) 及 ( B ) 為兩事件。假定 ( P(A)=0.8 )、( P(B|A)=0.45 ) 及 ( P(B|A')=0.6 ),其中 ( A' ) 為 ( A ) 的互補事件。求
(a) ( P(B) )
(b) ( P(A|B) )
(c) ( P(A\cup B) ).
(5分)
寫於邊界以外的答案,將不予評閱。
前往 DSE.zone 獲取更多試題
寫於邊界以外的答案,將不予評閱。
2018-M1 P.1 前往 DSE.zone 獲取更多試題
寫於邊界以外的答案,將不予評閱。

答案(英文)
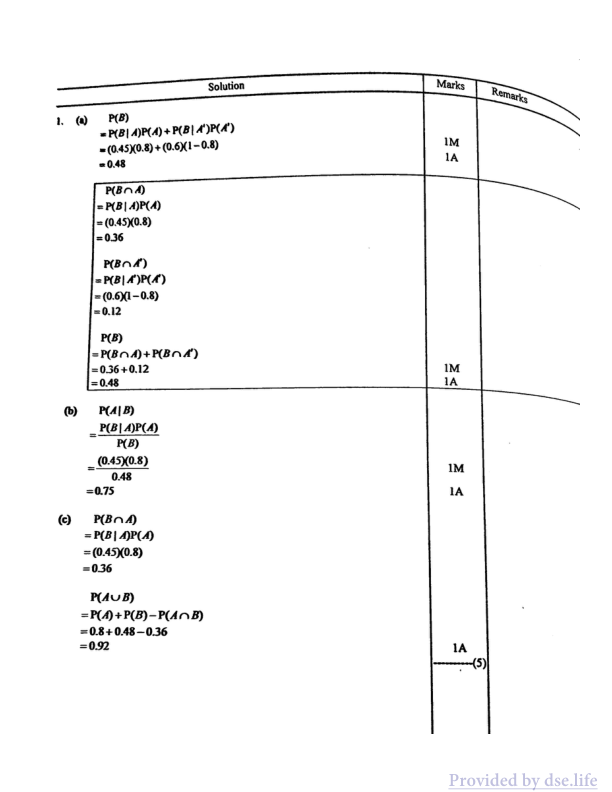
- (a) Solution: P(B) = P(B|A)P(A) + P(B|A')P(A') = (0.45)(0.8) + (0.6)(1 - 0.8) = 0.48 Marks: 1M 1A Remarks:
P(B∩A) = P(B|A)P(A) = (0.45)(0.8) = 0.36
P(B∩A') = P(B|A')P(A') = (0.6)(1 - 0.8) = 0.12
P(B) = P(B∩A) + P(B∩A') = 0.36 + 0.12 = 0.48 Marks: 1M 1A
(b) P(A|B) = \frac{P(B|A)P(A)}{P(B)} = \frac{(0.45)(0.8)}{0.48} = 0.75 Marks: 1M 1A
(c) P(B∩A) = P(B|A)P(A) = (0.45)(0.8) = 0.36
P(A∪B) = P(A) + P(B) - P(A∩B) = 0.8 + 0.48 - 0.36 = 0.92 Marks: 1A